Complex Chaos Game (CCG)

The CCG algorithm is a variation on the well known iterative rule for the Mandelbrot Set.

Z -> Z^2 + C

I start with Z(0)=0 but instead of choosing a constant C, I randomly choose the C from a

predetermined group of possible values.

Sometimes no more then 2 attractors are used and sometimes up to 17.

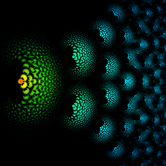
All the images below are generated from the exact same algorithm, they just use different C values.

Color corresponds to the distance each point is from the previous iteration.

Just below the image gallery you can find some code (written for Processing) for producing these fractals.

The code is a simple starting point and I encourage you to make your own iterations on it.

/// Simple Example Code for Complex Chaos Game (CCG) Algorithm
/// This can be MUCH expanded :-)
/// In this example I use only 2 Cs and they are strongly related, since one is the negative of the other.
/// This is the first example I stumbled upon, 25 years ago.

/// BASIC DESCRIPTION:
///===================
/// Start with a complex number Z=0;
/// Pre-choose 2 or more complex numbers to act as C in the folowing iteration rule:
/// Z -> Z^2 + C
///
/// This is of course Mandelbrot's iteration rule, but this time you randomly use

/// a different C for each iteration.
/// Draw the results along the way and that's it.

int max_iterations = 500000; // No. of iterations to perform
int n = 0; // iterations counter
float a, b = 0.0; // a,b are the Real and Imaginery parts of the would-be result.
int sc l= 800; // results are number less then 1 so let's scale it up.

float[] cr = new float[2]; // C[0] and C[1]'s real part.
float[] ci = new float[2]; // C[0] and C[1]'s imaginery part.

void setup() {

size(800, 800);
background(0);
colorMode(HSB);
strokeWeight(1);
noLoop();

cr[0] = 0.0; // Hard coded C values
ci[0] = 0.3;

cr[1] = 0.0;
ci[1] = -0.3;
}

void draw() {

while (n<max_iterations && abs(a)<2.0 && abs(b)<2.0)
{
// Calculate Complex Chaos Rule
float aprev = a; // save previous result to calculate distance later
float bprev = b;

float aa   = a*a; // These 3 lines perform squaring the complex number Z
float bb = b*b ;
float twoab = 2.0 * a * b ;

int r = int(random(2)); // Toss a coin and use result as index for C

// Result
a = aa - bb +cr[r] ;
b = twoab +ci[r] ;

//Draw points colored by distance from prev. point
float dst = dist(a, b, aprev, bprev);
float cl = map(dst, 0.0, 0.5, 0.0, 255.0);

set(int(width/2+a*scl), int(width/2 - b*scl), color(cl, 255, 255));
n++;
}

println("end");
}